20. 线段树-segmentTree

简介

什么是线段树呢？线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

线段树的每个节点都表示一个区间，而根据线段树的不同特征，线段树的节点值可以表示这个区间里的最小值，最大值或者sum值等等。

最小线段树

下面我们以最小线段树为例来说明一下线段树的特性：

如果原始数据是一个数组，我们也以数组来表示线段树。

假设生成的线段树的起点index=1，并且对线段树中的每个非叶子节点index k来说，它的左子节点index=2* k, 而它的右子节点index=2* k+1 。

上图中，标黄色的是原始数组，总共有七个元素。

上面的树形结构就是根据原始数组构建出来的线段树了。

因为是最小线段树，每个非叶子节点存储的都是子节点中的最小值。

举个例子： index=1 的元素表示的是原始数组范围0-6，并且它的值是11，表示的是原始数组0-6范围中，最小的值是11。

11的左子节点表示的范围是0-3，右字节点表示的范围是4-6。

可以看出线段树是一个平衡二叉树（不一定是完全平衡二叉树）。

线段树的叶子节点表示的就是原始数组的每一个值。

注意，这里线段树中范围的表示方式，是通过同时传入treeIndex和数组的左右边界来表示的。

线段树的构建

我们先来看一个线段树构建的动画：

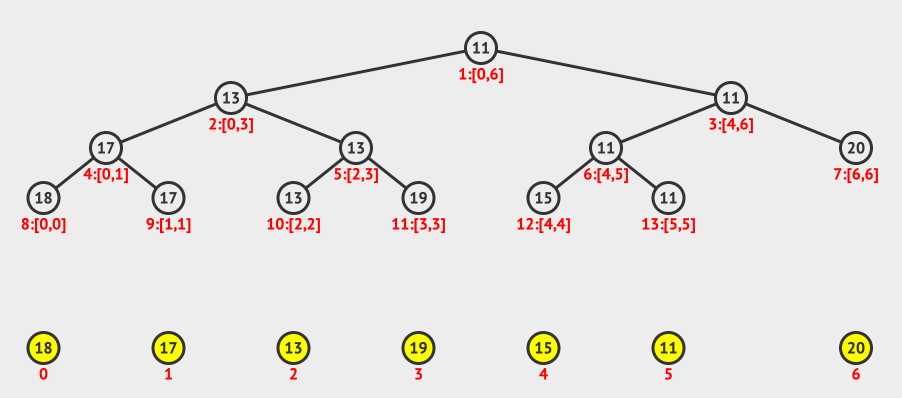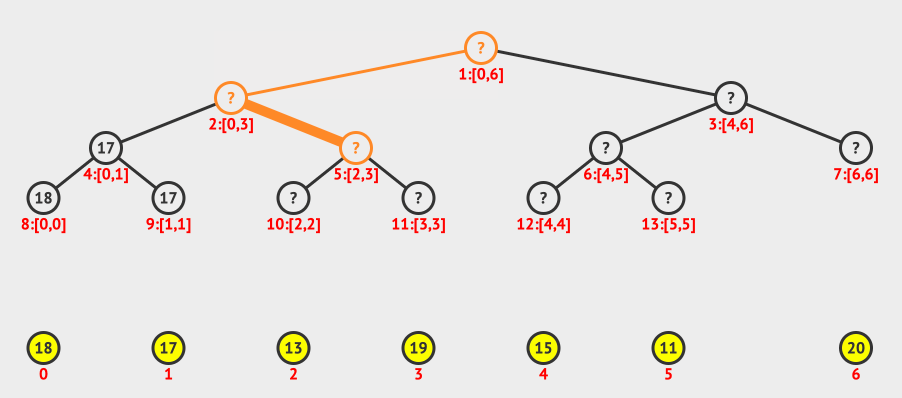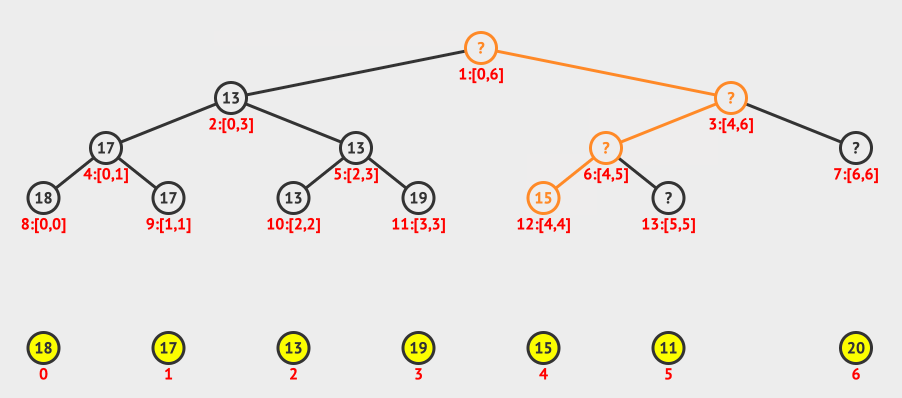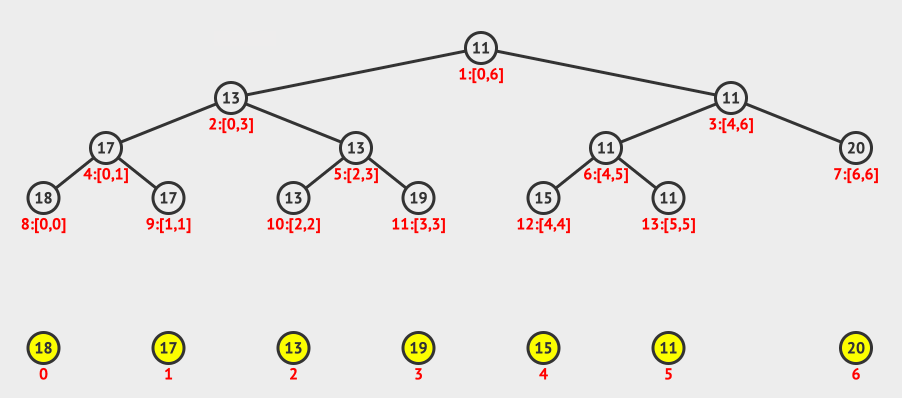
从上面的动画，我们可以看出我们使用的是递归构造的方法。

首先，我们定义两个数组：一个数组存放的是原始数组的引用，一个数组存放的是新生成的线段树。

新构建的segmentTree，对于满二叉树 最后一层的节点数乘以2 大致就是整棵树的节点数。

但是线段树并不一定是满二叉树，但是一定是平衡二叉树，所以需要多冗余一层。也就是 乘以4 就足以盛放所有的节点数。

新构建的segmentTree 以index=1为起点。

我们看一下构建线段树的代码：

   /**
     * 构建segmentTree
     * @param treeIndex 当前需要添加节点的索引
     * @param arrayLeft 数组的左边界
     * @param arrayRight 数组的右边界
     */
    private void build(int treeIndex, int arrayLeft, int arrayRight) {
        if (arrayLeft == arrayRight)   //如果相等则随便选择一个赋值
            segmentTree[treeIndex] = originalArray[arrayLeft];
        else {       // 否则分别构建左侧子树和右侧子树，并根据我们需要构建的segmentTree类型来设置当前节点的值
            build(left(treeIndex) , arrayLeft , (arrayLeft + arrayRight) / 2);
            build(right(treeIndex), (arrayLeft + arrayRight) / 2 + 1, arrayRight);
            int p1 = segmentTree[left(treeIndex)], p2 = segmentTree[right(treeIndex)];
            segmentTree[treeIndex] = (p1 <= p2) ? p1 : p2;
        } }

我们是递归调用build方法， 直到传入的arrayLeft == arrayRight，也就是说直到该节点是叶子节点的时候，就直接赋值。

如果不是叶子节点，则递归构建左子树和右子树。

最后构建他们的父节点，因为这里我们构建的是最小线段树，所以取两者的最小值。

线段树的搜索

先看一个动画：

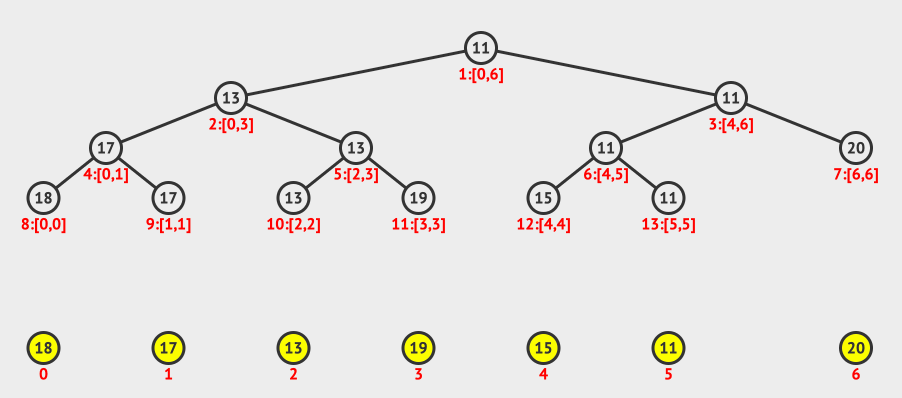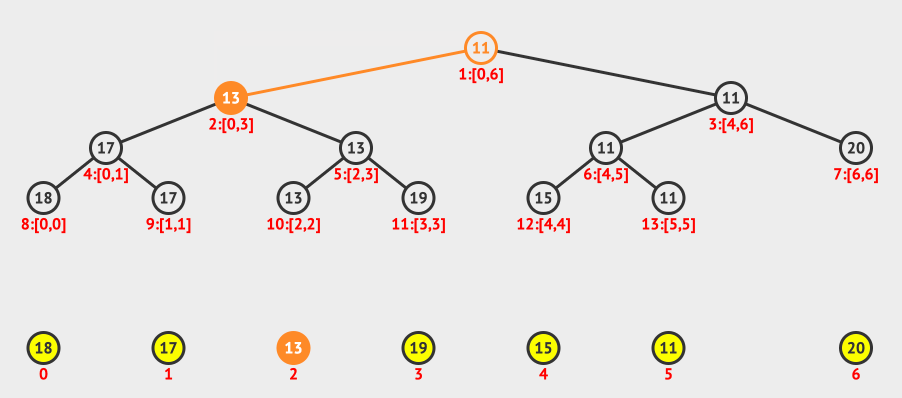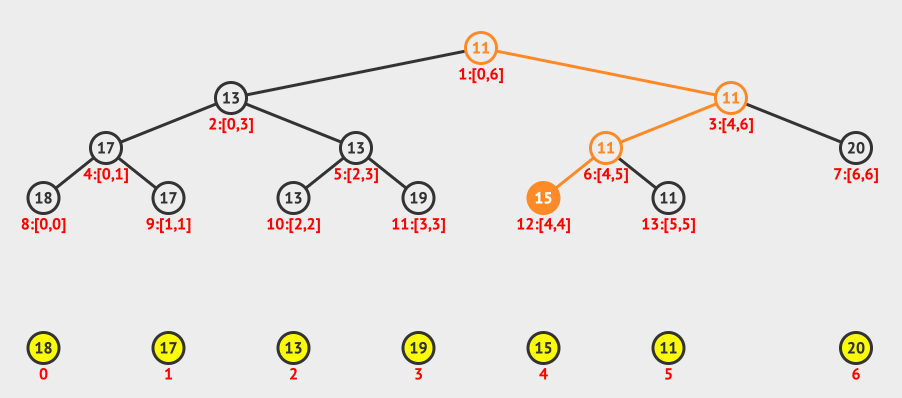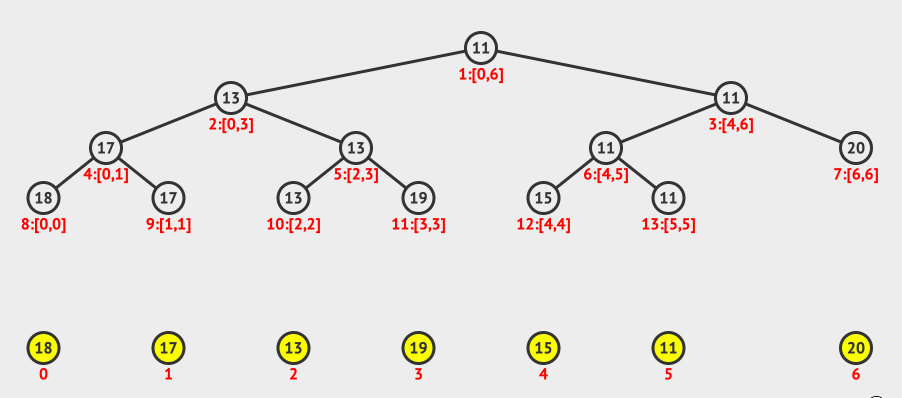
上图中，我们搜索的是2-4范围的最小值。

怎么求出来呢？

我们从index=1开始，先判断0-6是否在2-4的范围内，如果不是，则继续搜索左子树和右子树。

搜索左子树：判断0-3是否在2-4的范围内，发现部分重叠，则继续搜索左右子树。

搜索左子树：判断0-1是否在2-4的范围内，发现超出了范围，停止搜索左子树。

搜索右子树：判断2-3是否在2-4范围内，是，则直接返回该节点的值，也就是13。

同样的道理，我们可以得到右节点的返回值是15。

然后比较13和15，得到小的那个13。

用java代码实现如下：

    /**
     * 范围查询
     * @param treeIndex 当前要查找的节点index
     * @param arrayLeft 数组左边界
     * @param arrayRight 数组右边界
     * @param searchLeft 搜索左边界
     * @param searchRight 搜索右边界
     * @return
     */
    private int rangeQuery(int treeIndex, int arrayLeft, int arrayRight, int searchLeft, int searchRight) {
        if (searchLeft >  arrayRight || searchRight <  arrayLeft) return -1; // 搜索超出数组范围
        if (arrayLeft >= searchLeft && arrayRight <= searchRight) return segmentTree[treeIndex];  // 搜索的是整个数组范围，则直接返回根元素

        // 否则左右搜索
        int p1 = rangeQuery(left(treeIndex) , arrayLeft, (arrayLeft+arrayRight) / 2, searchLeft, searchRight);
        int p2 = rangeQuery(right(treeIndex), (arrayLeft+arrayRight) / 2 + 1, arrayRight, searchLeft, searchRight);

        if (p1 == -1) return p2;   // 如果超出范围，则返回另外一个
        if (p2 == -1) return p1;
        return (p1 <= p2) ? p1 : p2; }  //返回最小的那个

线段树的更新

那么线段树如何更新呢？

我们同样可以使用递归的更新方法，先分别更新左右两个子树，然后再更新他们的父节点。

递归的结束条件是什么呢？

当传入的arrayLeft=arrayRight并且等于要更新的arryIndex的时候，就需要更新叶子节点的segmentTree的值了。

java实现代码如下所示：

   /**
     * 更新数组中的某个节点
     * @param treeIndex 树的index
     * @param arrayLeft 数组左边界
     * @param arrayRight 数组右边界
     * @param arrayIndex 要更新的数组index
     * @param newValue 要更新的值
     * @return
     */
    private int updatePoint(int treeIndex, int arrayLeft, int arrayRight, int arrayIndex, int newValue) {
        // 设置i 和 j 等于要更新的数组index
        int i = arrayIndex, j = arrayIndex;

        // arrayIndex超出范围，则直接返回
        if (i > arrayRight || j < arrayLeft)
            return segmentTree[treeIndex];

        // 左右两个index相等
        if (arrayLeft == i && arrayRight == j) {
            originalArray[i] = newValue; // 找到要更新的index
            return segmentTree[treeIndex] = originalArray[i]; // 更新segmentTree
        }

        // 分别获得左右子树的最小值
        int p1, p2;
        p1 = updatePoint(left(treeIndex) , arrayLeft , (arrayLeft + arrayRight) / 2, arrayIndex, newValue);
        p2 = updatePoint(right(treeIndex), (arrayLeft + arrayRight) / 2 + 1, arrayRight , arrayIndex, newValue);

        // 更新treeIndex的值
        return segmentTree[treeIndex] = (p1 <= p2) ? p1 : p2;
    }

同样的道理，我们可以生成最大线段树和Sum线段树。

线段树的复杂度

求线段树的区间统计，时间复杂度和二叉树的高度有关系，和元素的个数没关系，它的时间复杂度为 O(log n)。

本文的代码地址：

learn-algorithm

本文收录于 www.flydean.com

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！